This weeks' Topic

Geometric Construction

Introduction:

The solution of many graphical problems requires the use of geometry and geometric construction. Graphical methods can be applied to solve some types of problems in algebra and arithmetic and virtually all types of problems in analytical geometry.

Angles:

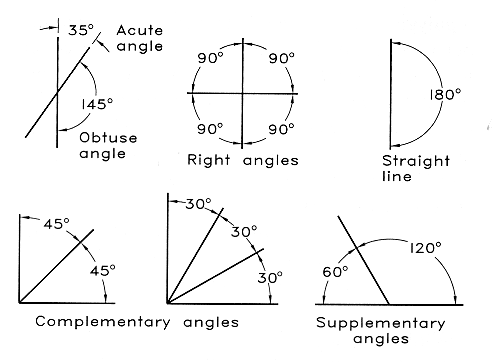
A fundamental application of geometric construction involves drawing lines at specified angles to each other. The unit of angular measurement is the degree. There are 360 degrees in a circle.

Polygons:

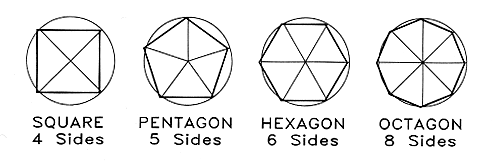
A polygon is a multi-sided plane figure of any number of sides. If the sides of a polygon are equal in length, the polygon is a regular polygon. A regular polygon can be inscribed in a circle and all its corners will lie on the circle.

Circles:

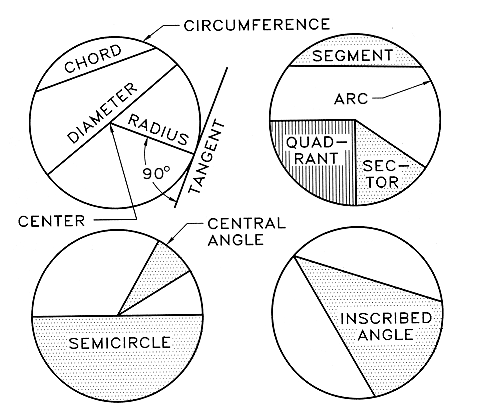
A circle is constructed by swinging a radius from a fixed point through 360. Figure 5.5 shows the names of the elements of a circle.

Constructing Polygons:

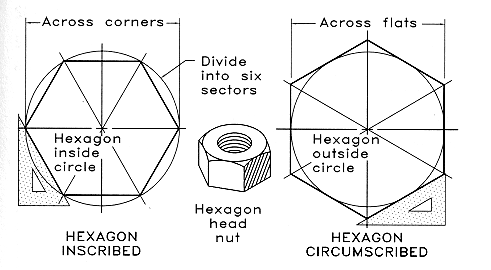
A regular polygon can be inscribed in of circumscribed about a circle. When it is inscribed, all corner points will lie on the circle. When it is circumscribed, all sides will lie tangent to the circle.

Bisecting Lines and Angles:

Lines:

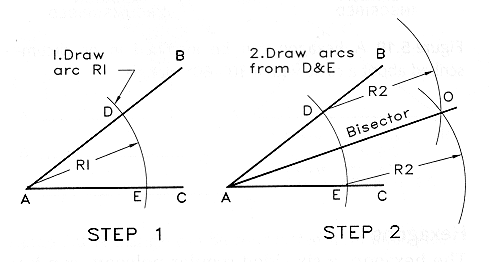
There are two methods of finding the midpoint of a line. In the first, a compass is used to construct a perpendicular bisector to a line. In the second, a standard triangle and a straight edge are used.

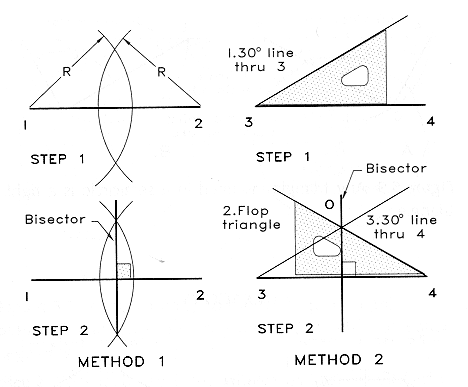
Angles:

You may bisect angles by using a compass and drawing three arcs as shown in below.

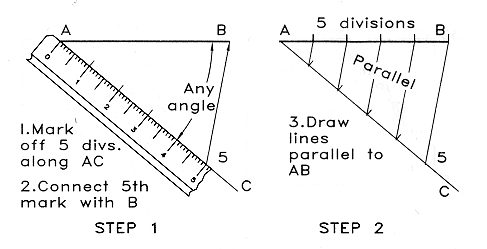
Division of Lines:

Dividing a line into several parts often is necessary, such as in the case of locating equally spaced lines on a graph.

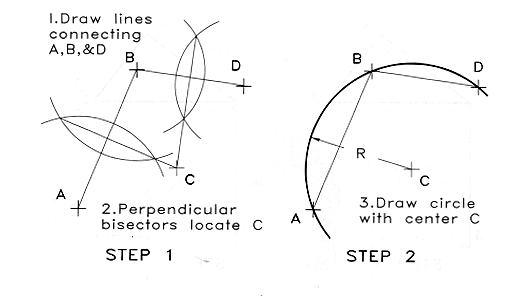
Arcs:

An arc may be drawn through three points by connecting the points with two lines and drawing perpendicular bisectors through each line to locate the center of the arc.

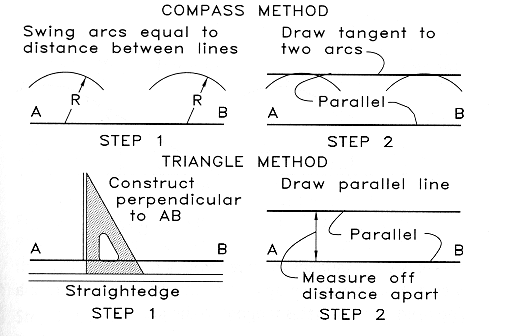
Parallel Lines:

A line may be drawn parallel to another by using either method shown below. Both of these methods may be used regardless of the angle at which the first line lies.

Points of Tangency:

A point of tangency is the theoretical point at which a line joins an arc or two arcs join without crossing.

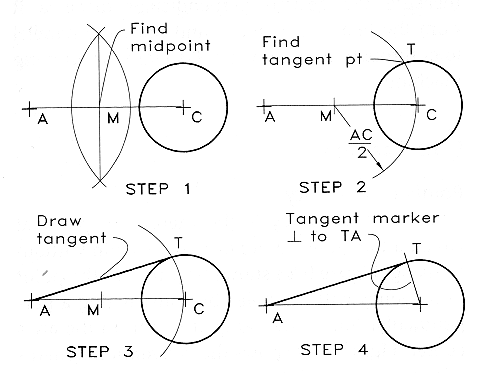
Line Tangent to an Arc:

This figure shows one way to find the point of tangency between a line drawn from point A and an arc.

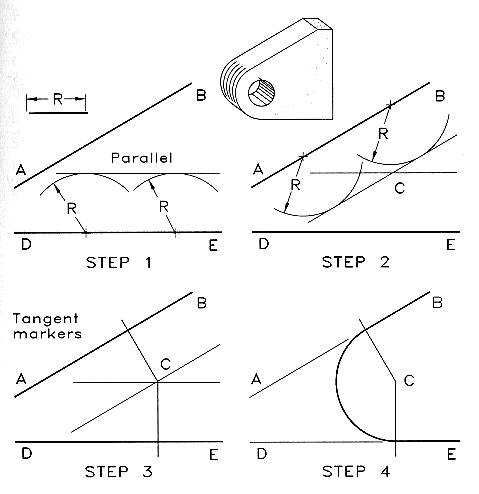
Arc Tangent to Two Lines:

Constructing an arc of a given radius tangent to two non-parallel lines that form an acute angle.

.

The same steps apply to constructing an arc tangent to two lines that form an obtuse angle.

Arc Tangent to an Arc and a Line:

See Figure 5.32 for the steps for constructing an arc tangent to an arc and a line, where the arcs turn away from each other. Figure 5.33 shows the method used when the arcs turn in the same direction.

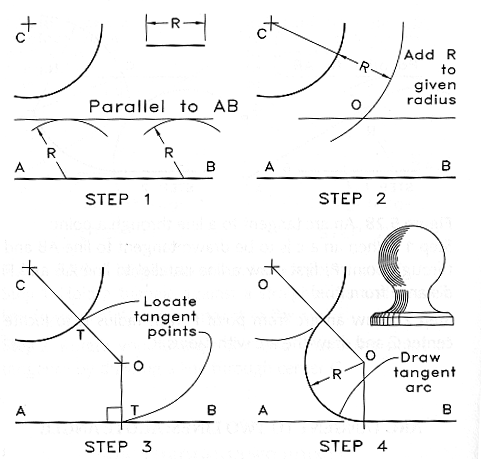
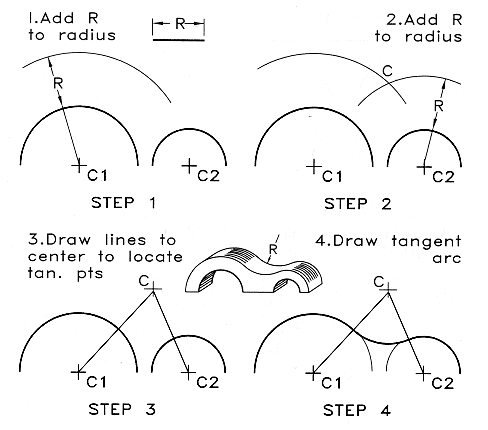
Arc Tangent to Two Arcs:

As above there are two possible directions which the tangent arc can go. This figure shows the steps used when the tangent arc is to be concave.

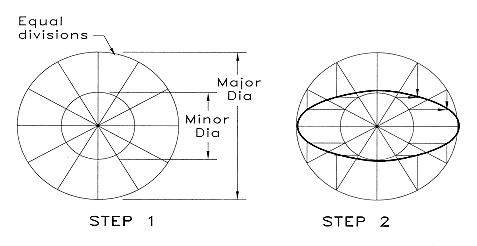
Ellipses:

The ellipse is a section formed by passing a plane through a cylinder at an angle. The two components of an ellipse are the major diameter and the minor diameter.

The major diameter is the same as the diameter of the cylinder, the minor diameter is a result of the angle at which the plane passes through the cylinder.

Below is an example of one method of constructing an ellipse.

• The techniques used in this sections is the foundation for your work with drawing instruments the rest of the semester